初试Finiate Automata之简单正则匹配

Why Study Automata Theory
There are several reasons why the study of automata and complexity is an
important part of the core of Computer Science…

摘自John E. Hopcroft, Rajeev Motwani, Jeffrey D. Ullman-Introduction to Automata Theory, Languages, and Computations-Prentice Hall (2006)

对于 Finiate Automata按照转移函数的不同可以分为确定型有穷自动机（Determinism Finite Automate, DFA），与非确定型有穷自动机（Non-determinism Finite Automate, NFA）。
本次主要拿DFA来练练手，不要一上来就想搞个大新闻 ，要由浅入深，循序渐进的学习，这样才能闷声发大财。

所以不要认为这些Too Young Too Simple 的东西不值一提，作为码农要提高自己的姿势水平。你们啊Navie

看题目：

// 考虑仅由字母{a, b}组成的字符串，要求字符串中字母b必须成对出现，
// 否则字符串非法。这个规则实现起来其实非常简单，不需要自动机也完全可以。
// 但是我们考虑使用自动机来进行判断。顺便，该规则的正规表达式描述是：(a|bb)*。
// 星号运算代表重复若干次，包括零次。

根据题目要求可以得出以下DFA有向图：

可知只有0号状态才是合法的。

程序初始为0状态，然后根据读入的字符进行状态变化，最终的状态若回到0就代表输入的字符串符合表达式要求，若为其他状态则不符合要求。

那么用什么来表达这种数据结构呢？

首先想到的就是邻接矩阵啊，用它来存储图还是比较方便的蛤蛤！

但在实际操作的过程中发现对于2号状态有两条从自己出发指向自己的弧，这种情况使用邻接矩阵就不是很容易表示了。所以果断放弃邻接矩阵方式存储，

转而选用邻接表来存储这个DFA有向图。

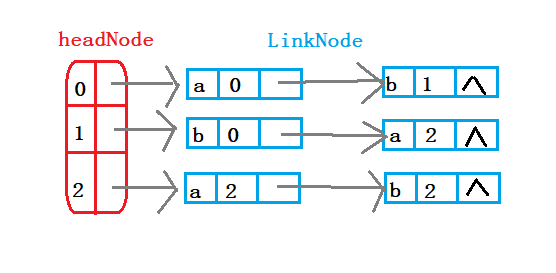
//  @Authour : Michael Jiang 2019年9月22日

#include <iostream>
#include <cstring>

struct LinkNode
{
    char weight;                //状态之间转换的条件
    struct headNode *nextStatus;//下一个状态的节点
    struct LinkNode *next;      //下一个同弧尾节点
    LinkNode(char w, headNode *ns):  
        weight(w),nextStatus(ns),next(NULL){}
};

struct headNode
{
    int statusID;               //状态标志
    struct LinkNode *next;      //从该状态指出的所有弧节点
};

    headNode *head = new headNode[3];

// 生成相应的确定性有穷自动机
void makeDFA()
{

    for (size_t i = 0; i < 3; i++)
    {
        head[i].statusID = i;
    }
    LinkNode *p;
    p = new LinkNode('a', &head[0]);
    head[0].next = p;
    p->next = new LinkNode('b', &head[1]);

    p = new LinkNode('b', &head[0]);
    head[1].next = p;
    p->next = new LinkNode('a', &head[2]);
    
    p = new LinkNode('a', &head[2]);
    head[2].next = p;
    p->next = new LinkNode('b', &head[2]);
    
}

// 判断输入的字符串str是否符合规则
bool isLegal(const char *str)
{
    int nowStatus = 0;
    for (size_t i = 0; i < strlen(str);i++)
    {
        LinkNode *p;      
        p = head[nowStatus].next;
        while(p){
            if(p->weight == str[i]){            
                nowStatus = p->nextStatus->statusID;
                break;
            }
            p = p->next;
        }    
    }
    return nowStatus==0;
}


int main(int argc, char const *argv[])
{
    const char *str[6] ={
         "abb",
         "aaabb",
         "bbaa",
         "bab",
         "aba",
         ""
    };

    //构造确定性有穷自动机
    makeDFA();

    for (size_t i = 0; i < 6; i++)
    {
        printf("str[%d] = %s \t: isLegal=%d\t\n",i,str[i],isLegal(str[i]));
    }
    return 0;
}

执行结果：

C:\Users\Michael Jiang\Desktop\Automata>g++ main.cpp && a.exe
str[0] = abb    : isLegal=1
str[1] = aaabb  : isLegal=1
str[2] = bbaa   : isLegal=1
str[3] = bab    : isLegal=0
str[4] = aba    : isLegal=0
str[5] =        : isLegal=1