卡尔曼滤波(Kalman filter)是一种高效率的递归滤波器(自回归滤波器),它能够从一系列的不完全及包含噪声的测量中,估计动态系统的状态。卡尔曼滤波会根据各测量量在不同时间下的值,考虑各时间下的联合分布,再产生对未知变数的估计,因此会比只以单一测量量为基础的估计方式要准。卡尔曼滤波得名自主要贡献者之一的鲁道夫·卡尔曼。
卡尔曼滤波建立在线性代数和隐马尔可夫模型(hidden Markov model)上。其基本动态系统可以用一个马尔可夫链表示,该马尔可夫链建立在一个被高斯噪声(即正态分布的噪声)干扰的线性算子上的。系统的状态可以用一个元素为实数的向量表示。随着离散时间的每一个增加,这个线性算子就会作用在当前状态上,产生一个新的状态,并也会带入一些噪声,同时系统的一些已知的控制器的控制信息也会被加入。同时,另一个受噪声干扰的线性算子产生出这些隐含状态的可见输出。
所以 kalman filter 要求环境噪声是满足高斯分布的,且系统是线性的假设之下,这点对于工程实际应用是难以满足的,所以针对这一问题,研究者们又基于kalman filter 提出了扩展卡尔曼滤波器(Extended Kalman Filter,简称EKF)中状态转换和观测模型不需要是状态的线性函数,可替换为(可微的)函数。
简单测试:
一、 背景介绍
假设一小车作匀加速运动,初速度为0,加速度为5米每二次方秒,小车上装有速度传感器,采样频率为10Hz,传感器测量噪声为高斯白噪声,需要充分利用这些信息来估计车辆的速度状态,并验证卡尔曼滤波算法的实验原理与过程。
二、卡尔曼滤波原理
早在近百年前,就有人开始采用状态变量模型研究随机过程,随后为了解决对非平稳、多输入输出随机序列的估计问题,卡尔曼提出了递推最优估计理论。它采用状态空间法描述系统,由状态方程和测量方程组成,即知道前一个状态的估计值和最近一个观测数据,采用递推算法估计当前的状态值。其具有以下特点:
(1) 算法是一个递推过程,且状态空间法采用在时域内设计滤波器的方法,因而适用于多维随机过程的估计;离散型卡尔曼滤波算法适用于计算机处理。
(2) 采用递推算法计算,不用知道所有过去的值,用状态方程描述状态变量的动态变化规律,卡尔曼滤波同样适用于非平稳过程。
如图所示,为卡尔曼滤波算法的实现流程图,其基本思路是若有一组强而合理的假设,给出系统的历史测量值,可以建立最大化这些早前测量值的后验概率的系统状态模型。其基本假设是被建系统是线性的,影响测量的噪声属于符合高斯分布的白噪声。
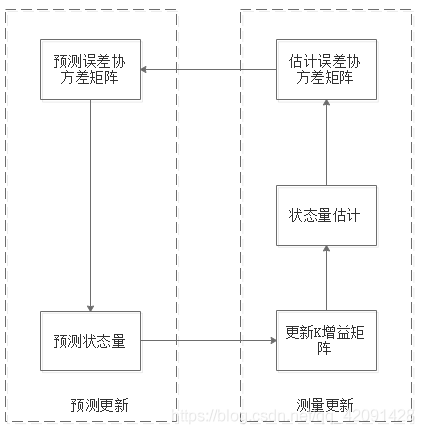
三、卡尔曼滤波的状态方程和测量方程
整个实现过程包含预测更新和测量更新两大部分。
(1) 预测更新:
预测状态量:\(\hat X(t|t-1)=A \hat x (t-1)+Bu(t)\)
预测误差协方差矩阵:\(P(t|t-1)=AP(t-1)A^\top +Q\)
(2) 测量更新:
最优估计状态量:\(\hat X(t)=\hat x(t|t-1) + K(t)[z(t)-H \hat x(t|t-1)\)
计算误差增益:\(K(t)=\frac{P(t|t-1)H^\top}{R+HP(t|t-1)H^\top}\)
误差协方差矩阵:\(P(t)=[I-K(t)H]P(t|t-1)\)
设k时刻小车速度为 ,则系统状态方程为:\(x_k=x_{k-1}+0.5+w_{k-1}\)
测量方程为:\(z_k=x_k+v_k\)
结合卡尔曼滤波算法的预测和测量更新流程,可有:\(A=[1]; B=[1]; u=0.5; Q=E(ww^\top); H=[1]; R=E(vv^\top)\)
四、结果分析
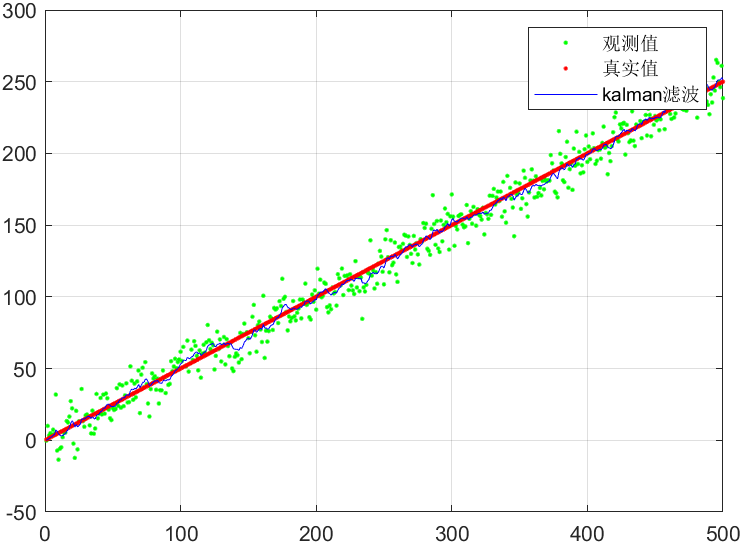
根据以上理论分析,完成相应matlab程序(代码见参考),并画出小车速度的观测值、真实值、滤波值的对比曲线图如下:
参考:
- https://blog.csdn.net/qq_42091428/article/details/105643181
- https://en.wikipedia.org/wiki/Kalman_filter








