调频连续波(Frequency Modulated Continuous Wave, FMCW)，是指雷达的发射器以一个变化的频率来发射某种电磁波，FMCW雷达的信号调制主要包括三角波调制、锯齿波调制、正弦波调制等几种不同的方式。由于正弦波调制检测物体时需要调节信号频偏，大多应用于只有一个探测目标的情况，比如高度计。FMCW雷达需要检测距离和速度等信息，而且通常希望检测多个目标，所以大多采用三角波调制和锯齿波调制。锯齿波调制主要用来测量物体的距离，而三角波调制可以同时得到物体的距离和速度信息。
毫米波雷达由发射机、天线、接收机和处理单元组成。发射机发射波长为1~10mm、频率为30GHZ-300GHZ的电磁波，目标反射的电磁波由雷达接收机接收，处理单元使用获得的信号来确定目标距离速度。毫米波雷达通过时差法（Time of flight, ToF）来进行测量，具体来说雷达发射毫米波后若存在障碍物会反射毫米波，由于光速已知，雷达可以通过计算往返时间来得到目标距离。
对于相对于雷达的静止物体，我们可以通过如下方式来测量该物体距雷达的距离。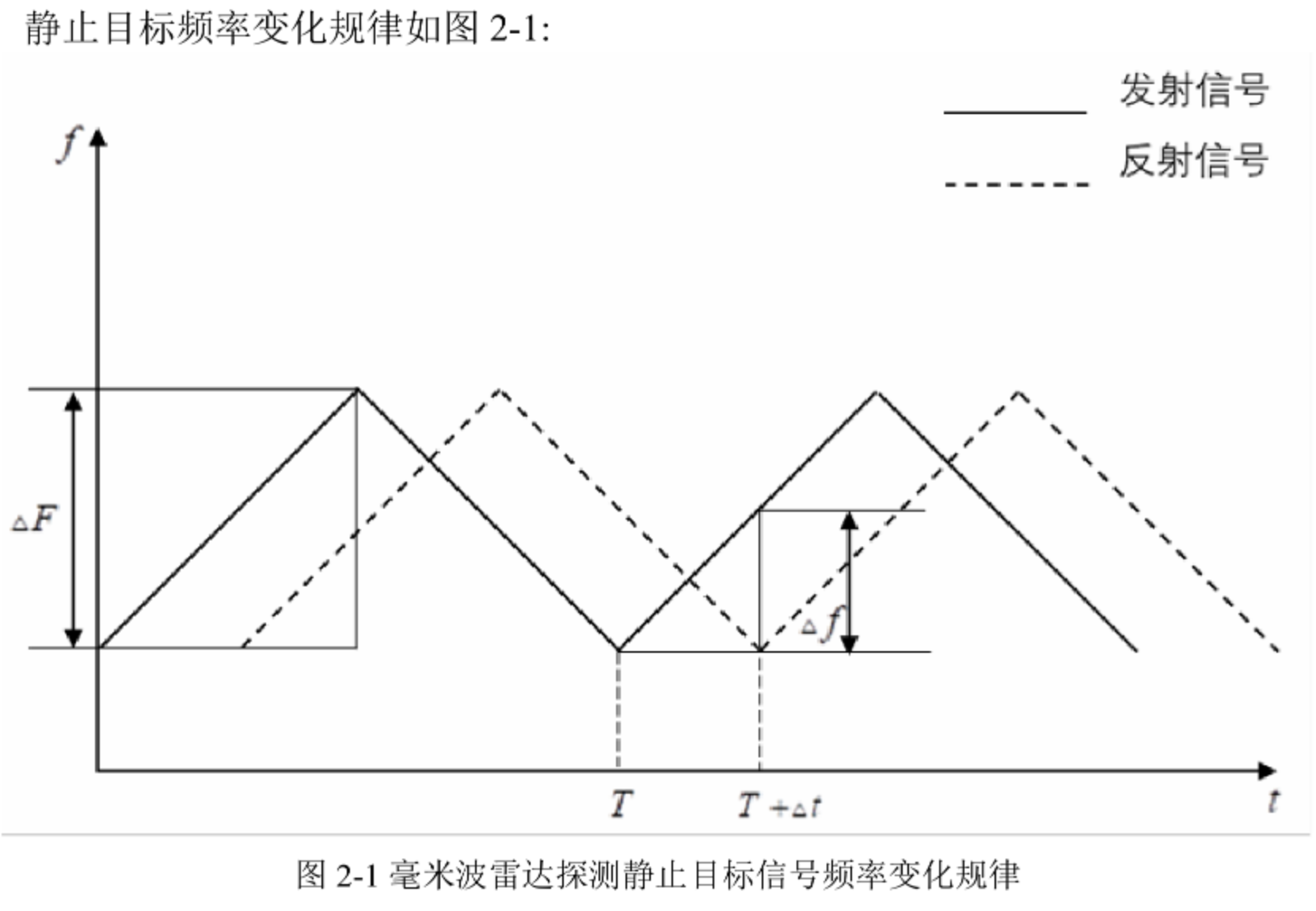
运动目标频率变化规律如图所示：
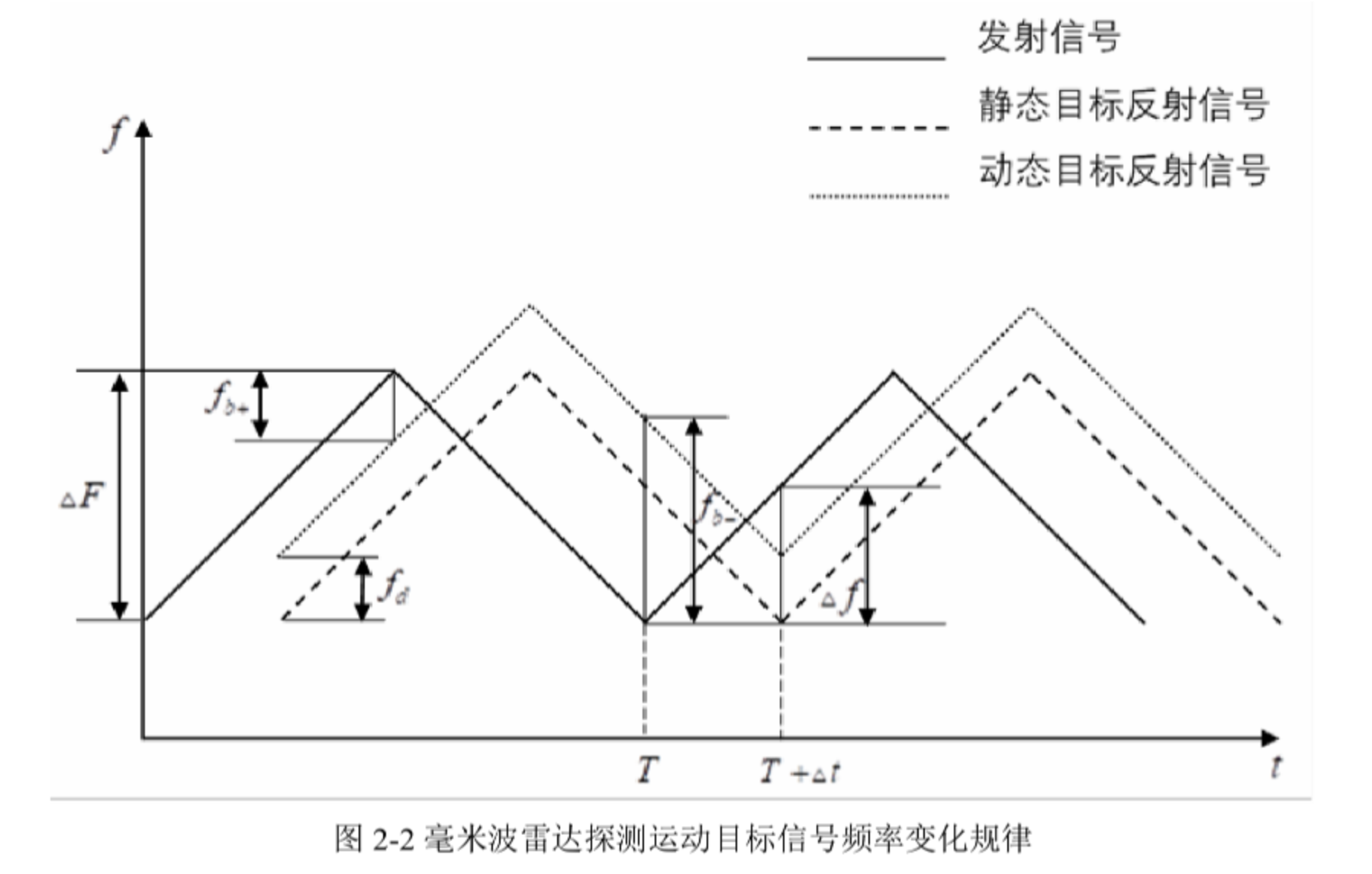
由以上方法即可得到雷达探测目标的距离与速度。
这里，对于公式(2-9)所提到的多普勒频移，这里我还想再说明一下。
\(f_d=f_R-f_T \tag{1}\)
(1)中\(f_d\)表示多普勒频移，\(f_R\)表示目标回波的频率(Hz)，\(f_T\)表示发射信号的频率(Hz)。多普勒频移的表达式为：
\(f_d=\frac{2v}{λ} \tag{2}\)式中， λ 为信号波长(m)，v为雷达与目标间的相对径向速度(m/s)。这是一个近似的表达式，适用于目标相对于雷达的径向速度远小于电磁波传播速度的情况。实际情况往往如此，因此通常用(2)式来计算目标的径向速度。
多普勒效应是由奥地利数学家多普勒首先发现和提出的，它反映了信号频率与运动速度之间的关系。值得注意的是这里的速度指相对的径向速度，即运动速度沿二者直线方向的分量。
下面对多普勒频移的表达式(2)作一个简单的推导。
雷达发射一段正弦波，起始点为A,终止点为B,在空间延伸的长度为D,频率为 f 0 f_0 f0.目标以径向速度 v r v_r vr向着雷达飞行（远离雷达飞行时速度为负数，原理相同）,如图所示：
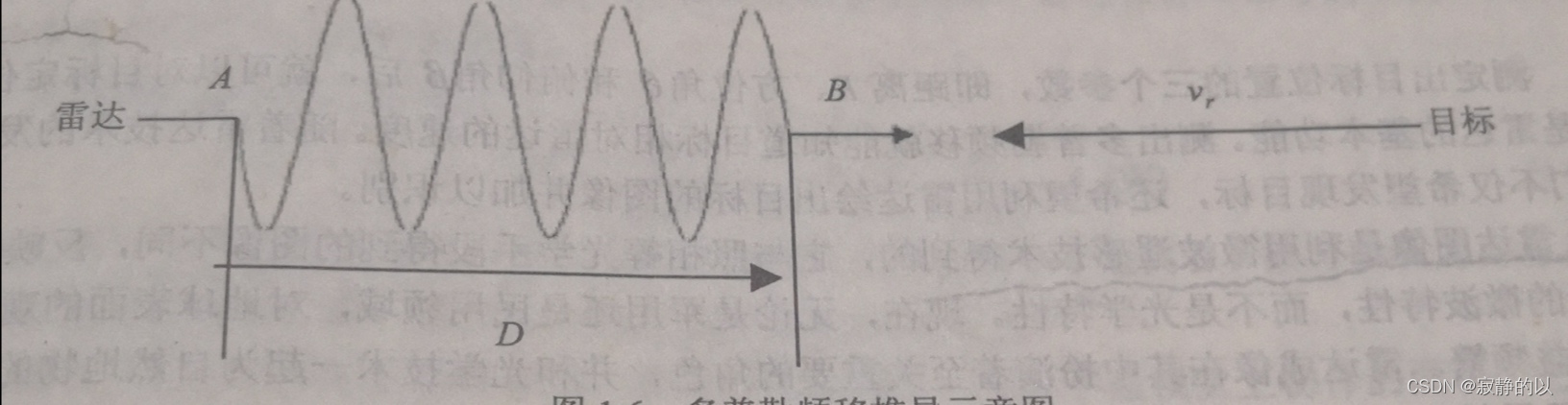由于目标向雷达运动，B点接触目标后，到A点接触目标，所需的时间 Δt为：
当A点接触目标时，B点相对于目标的距离就是反射后正弦波的长度 D′，其计算式为：
\(D′=(c-v_r) \cdot Δt=\frac{c-v_r}{c+v_r} \cdot D \tag{4}\)其中 \(c-v_r\)表示B点反射后的电磁波相对目标的速度。反射后的正弦波长度小于反射前的长度，但波的个数是不变的，设反射后的频率为\(f’_0\),则有：
\(\frac{f’_0}{f_0}=\frac{D}{D’}=\frac{c+v_r}{c-v_r}=1+\frac{2v_r}{c-v_r} ≈1+\frac{2v_r}{c} \tag{5}\)上式成立的条件是电磁波传播速度远大于目标运动速度，实际情况中通常如此，则多普勒频移\(f_d\)为：
\(f_d=f’_0 – f_0 = f_0 \cdot \frac{2v_r}{c}=\frac{2v_r}{λ}\tag{6}\)
参考
- 基于毫米波雷达与摄像头并联融合的车辆检测跟踪研究_郭熙
- https://baike.baidu.com/item/%E8%B0%83%E9%A2%91%E8%BF%9E%E7%BB%AD%E6%B3%A2%E9%9B%B7%E8%BE%BE/1710951
- https://blog.csdn.net/m0_47867419/article/details/123117892