设毫米波雷达给出的目标数据为\((ρ,θ)\)即目标的距离和方位角。图像给出的数据为\((u,v)\)即目标在图像上的横坐标值和纵坐标值。
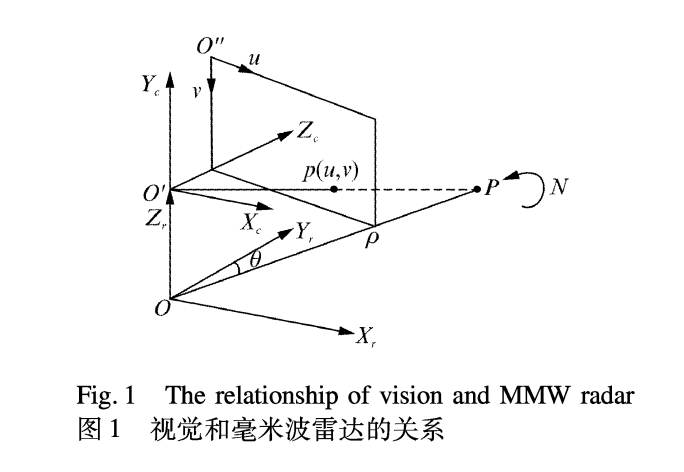
其中\(O’X_rY_rZ_r\)表示雷达的坐标系,\(O’X_cY_cZ_c\)表示相机的坐标系,\(O”uv\)表示图像的坐标系。则\((ρ,θ)\)和\((u_c,v_c)\)之间存在以下关系式:
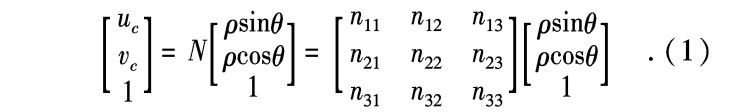
其中\(N\)是待定的,待会使用最小二乘法估计出。
对于图像上的某个目标,它可能由多个形如\((u,v)\)的点组成,我们使用\(f(u,v)\)表示图像中该点的像素值,则目标的形心可以表示为:
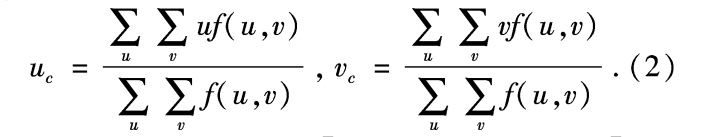
这样的目标点可能有多个,我们将其记为:
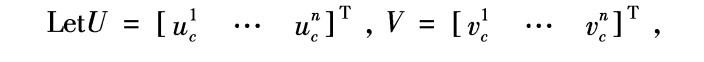
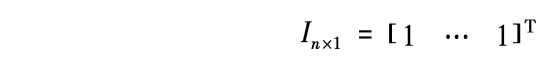
根据(1)式,我们将\(u_c\)单独取出计算可得下式:
\(u^1_c=n_{11}ρ^1sinθ^1+n_{12}ρ^1cosθ^1+n_{13}\\u^2_c=n_{11}ρ^2sinθ^2+n_{12}ρ^2cosθ^2+n_{13}\\ … … \\ u^n_c=n_{11}ρ^nsinθ^n+n_{12}ρ^ncosθ^n+n_{13}\)那末,对于\(U\)有如下形式:
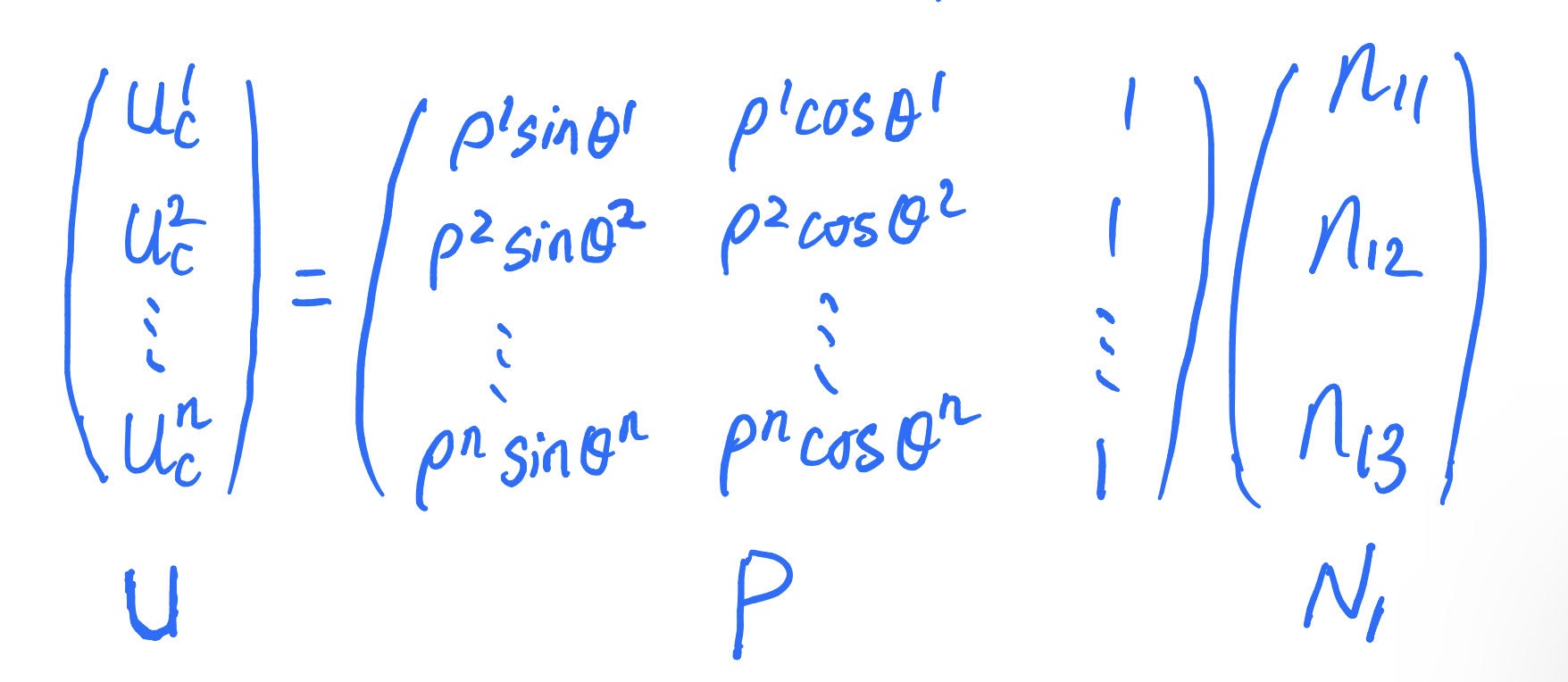
可以得到\(U=PN_1\),下面使用最小二乘法来估计\(N_1\)。
\(min||U-P \cdot N_1||_2 \tag{3} \)对\(N_1\)求导得
\(2(U-P \cdot N_1) \cdot P = 0 \tag{4} \)因为\(P\)不为0,所以化简(4)式得
\(U=PN_1 \tag{5} \)(5)式两边同乘\(P^T\)
\(P^TU=P^TPN_1 \tag{6} \)再整理得
\(N_1=(P^TP)^{-1}P^TU \tag{7} \)同理得:
\(N_2=(P^TP)^{-1}P^TV \tag{8} \) \(N_3=(P^TP)^{-1}P^TI \tag{9} \)又因为\(N=\begin{bmatrix}N_1^T \\N_2^T \\N_3^T\end{bmatrix}\)
所以\(N=\begin{bmatrix}((P^TP)^{-1}P^TU)^T \\((P^TP)^{-1}P^TV)^T\\((P^TP)^{-1}P^TI)^T\end{bmatrix}\)
由此便求出了(1)式中的\(N\) ,之后便可以将任意的雷达数据\((ρ,θ)\)转换为图像数据\((u_c,v_c)\)上了。
参考
- https://dl.acm.org/doi/abs/10.1145/3268866.3268868
- https://www.opticsjournal.net/Articles/OJ141106000194Xux4z7/Abstract
- https://blog.csdn.net/W1995S/article/details/118153146








