栈,复杂到简单。 ——Michael Jiang
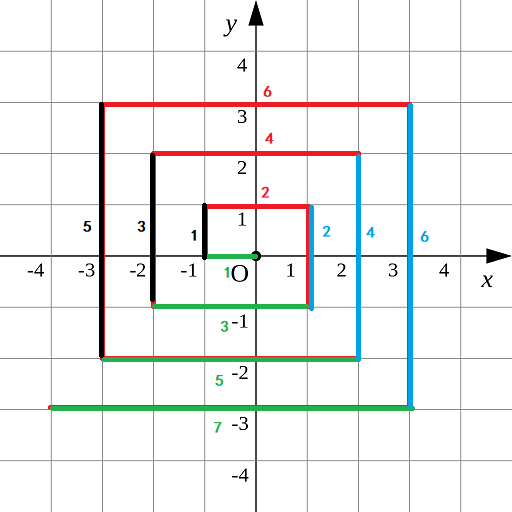
题目:

分析一波:
仔细观察3,4 它们是配对括号,中间没有其他括号;那么我们就可以消除它们;同理5,6 也是。
经过消除操作现在括号序列变成了:
[ ( ) ]
1 2 7 8
继续执行上述操作,最终可以消除全部括号。
如果最后还剩有无法消除的括号则说明给出的括号序列不合法!
开始操作:
1.我们首先把第一个括号推到栈中
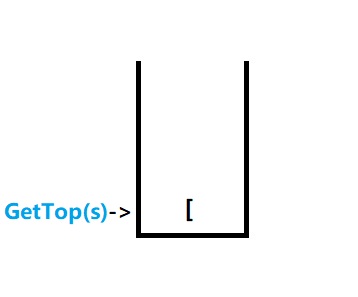
2.然后算出它的另一半存在变量need中,表示需求
很明显 need = ‘]’
3.准备推入第二个括号
第二个括号为 ( ;它不等于 need ,不能消去,只能入栈。
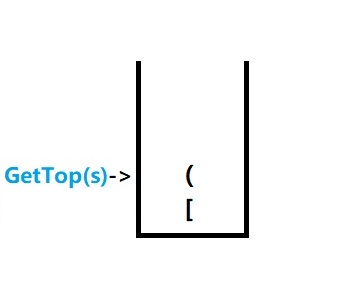
这时 need = ‘)’
4.准备第三个括号,同3步骤一样。
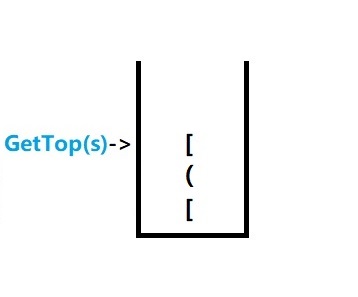
这时 need = ‘]’
5.准备第四个括号,发现第四个括号 ] 和 need 相同;那第四个就不要入栈了,直接扔掉。
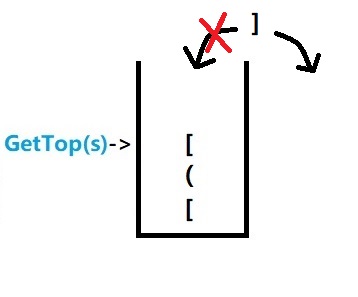
然后还要把栈顶的括号 [ 弹出 栈顶下移
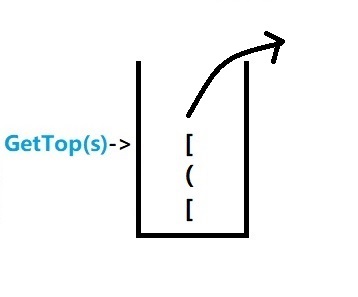

这时 need = ‘)’
6.继续插入第五个括号 [

这时 need = ‘]’
7.继续插入第六个括号 ] 发现第六个括号 ] 和 need 相同;那第六个就不要入栈了,直接扔掉。

然后还要把栈顶的括号 [ 弹出 栈顶下移

这时 need = ‘)’
8.继续插入第七个括号 ) 发现第七个括号 ) 和 need 相同;那第七个就不要入栈了,直接扔掉。
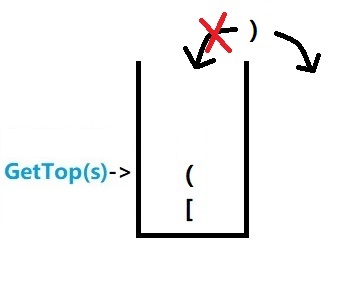
然后还要把栈顶的括号 ( 弹出 栈顶下移
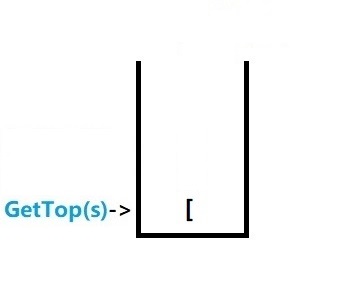
这时 need = ‘[‘
9.继续插入第八个括号 ] 发现第八个括号 ] 和 need 相同;那第八个就不要入栈了,直接扔掉。
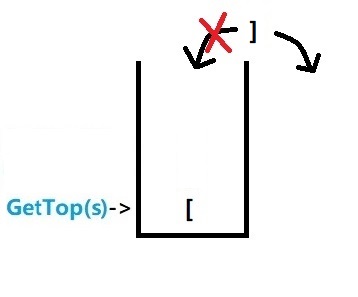
然后还要把栈顶的括号 [ 弹出 栈顶下移
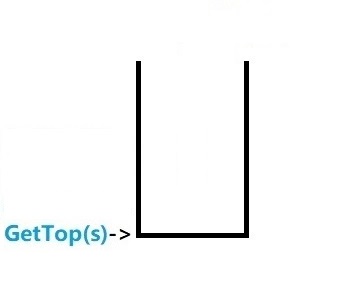
最终我们得到一个 空栈 即该括号序列为合法序列。
下面是实现代码(把栈精简了一下,删掉了一些没有用到的函数)
/************************
*Stack application [括号配对合法性检查]
*SENCOM LAB
*Michael Jiang
*2018-9-18
************************/
#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
#define ElemType char //这里直接根据需求改数据类型
#define STACK_INIT_SIZE 10
#define STACKINCREMENT 5
#include "stdio.h"
#include "stdlib.h"
typedef struct {
ElemType *base;
ElemType *top;
int stacksize;
}SqStack;
//active funtion
int InitStack(SqStack &s)
{
s.base = (ElemType *)malloc(sizeof(ElemType)*STACK_INIT_SIZE);
if(!s.base) return ERROR;
s.top = s.base;
s.stacksize = STACK_INIT_SIZE;
return OK;
}
ElemType GetTop(SqStack &s)
{
ElemType e;
if(s.top == s.base) return ERROR;
e = *(s.top-1);
return e;
}
int Push(SqStack &s,ElemType e)
{
if(s.top - s.base >= s.stacksize) {
s.base = (ElemType *)realloc(s.base,(s.stacksize+STACKINCREMENT)*sizeof(ElemType));
if(!s.base)exit(-1);
s.top = s.base + s.stacksize;
s.stacksize += STACKINCREMENT;
}
*s.top = e;
s.top++;
return OK;
}
int Pop(SqStack &s)
{
if(s.top == s.base) return ERROR;
s.top--;
return OK;
}
//Static funtion
int StackEmpty(SqStack s)
{
if(s.top == s.base)
return TRUE;
else
return FALSE;
}
int StackTravel(SqStack s)
{
ElemType *p = s.top;
printf("top->");
for(p--;p >= s.base ; p--)
{
printf("%c->",*p);
}
printf("base\n");
return OK;
}
//main funtion
int main(int argc, char const *argv[]) {
/* code */
int i;
char test[32],need = '?';
printf("INPUT:");
gets(test);
SqStack s; //构造栈
if(!InitStack(s)) exit(-1); //初始化
Push(s,test[0]); //先让第一个括号入栈
switch(GetTop(s)){ //根据栈顶括号找配对的另一半存入need中
case '[':need = ']';break;
case '(':need = ')';break;
}
for(i=1;test[i]!='\0';i++){ //开始循环
if(need == test[i]){ //判断准备入栈的括号是否为 need
Pop(s); //如果是;就将当前栈顶的括号弹出,执行下个循环
}
else{
Push(s,test[i]); //如果不是;就将这个括号入栈
}
switch(GetTop(s)){ //不管是不是;need一直是栈顶配对的括号
case '[':need = ']';break;
case '(':need = ')';break;
}
}
//StackTravel(s);
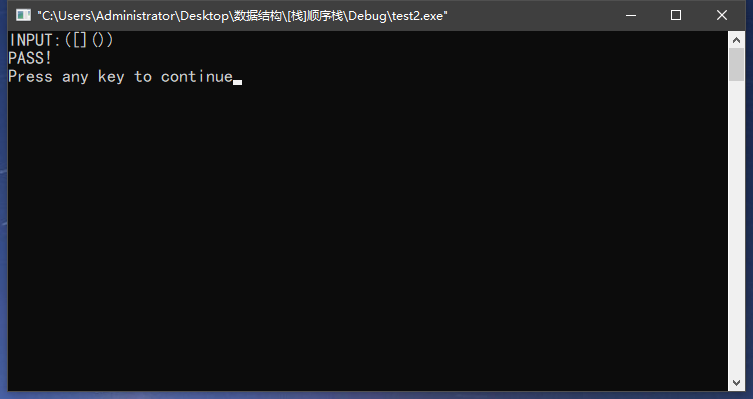
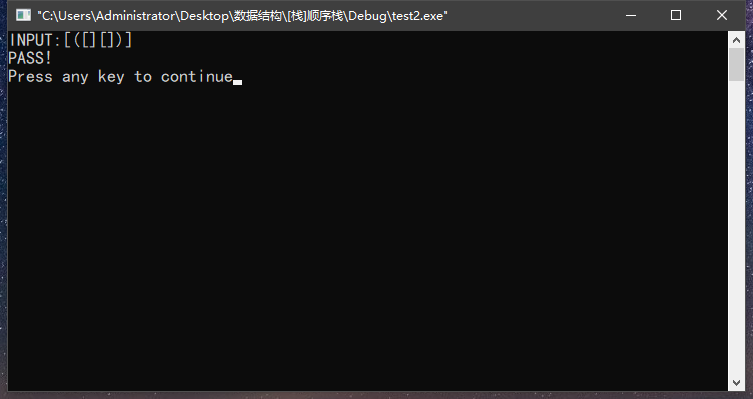
if(StackEmpty(s))//如果最后栈为空则通过合法性检查;否则未通过
printf("PASS!\n");
else
printf("FAIL!\n");
return 0;
}
END