螺旋折线

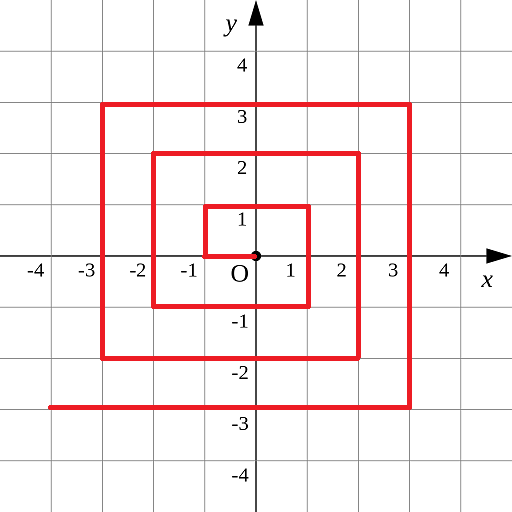
如图所示的螺旋折线经过平面上所有整点恰好一次。
对于整点(X, Y)，我们定义它到原点的距离dis(X, Y)是从原点到(X, Y)的螺旋折线段的长度。

例如 dis(0, 1)=3, dis(-2, -1)=9

给出整点坐标(X, Y)，你能计算出dis(X, Y)吗？

【输入格式】
X和Y

对于40%的数据，-1000 <= X, Y <= 1000
对于70%的数据，-100000 <= X， Y <= 100000
对于100%的数据, -1000000000 <= X, Y <= 1000000000

【输出格式】
输出dis(X, Y)

【样例输入】
0 1

【样例输出】
3

资源约定：
峰值内存消耗（含虚拟机） < 256M
CPU消耗 < 1000ms

请严格按要求输出，不要画蛇添足地打印类似：“请您输入…” 的多余内容。

注意：
main函数需要返回0;
只使用ANSI C/ANSI C++ 标准;
不要调用依赖于编译环境或操作系统的特殊函数。
所有依赖的函数必须明确地在源文件中 #include <xxx>
不能通过工程设置而省略常用头文件。

提交程序时，注意选择所期望的语言类型和编译器类型。

思路：

定义一个now(x,y)结构体存储当前位置初始化为(0,0) ;然后模拟螺旋过程并记录步数。

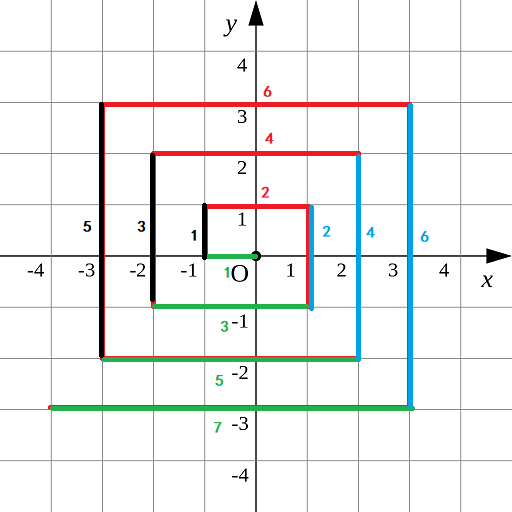
如图所示进行分解

int down_step  = 1;//绿线
int left_step  = 1;//黑线
int up_step    = 2;//红线
int right_step = 2;//蓝线

可以得出如下规律：

黑线和绿线都是按照 1,3,5,7… … 规律增加

红线和蓝线都是按照2,4,6,8… … 规律增加

可以总结为：

当前位置初始化为(0,0)

只要目标位置和当前位置不一致：

就按照 绿线->黑线->红线->蓝线 这个顺序走下去

每走一个循环 黑线和绿线按照 1,3,5,7… … 规律增加；红线和蓝线按照2,4,6,8… … 规律增加。

源码如下：

#include "cstdio"
#include "algorithm"

typedef struct {
	int x;
	int y;
}Pos;
Pos now={0,0};	//当前位置


int x, y;	//目标位置
int len = 0;	//移动的距离（最终答案）

int turn_down_line(int down_step)
{
	for(int i = 1; i <= down_step; i++)//模拟在 down_line 这条线上一步一步移动
	{
		now.x -= 1;
		len++;
		if(now.x == x && now.y == y)
			return 1;
	}
	return 0;
}
int turn_left_line(int down_step)
{
	for(int i = 1; i <= down_step; i++)
	{
		now.y += 1;
		len++;
		if(now.x == x && now.y == y)
			return 1;
	}
	return 0;
}
int turn_up_line(int down_step)
{
	for(int i = 1; i <= down_step; i++)
	{
		now.x += 1;
		len++;
		if(now.x == x && now.y == y)
			return 1;
	}
	return 0;
}
int turn_right_line(int down_step)
{
	for(int i = 1; i <= down_step; i++)
	{
		now.y -= 1;
		len++;
		if(now.x == x && now.y == y)
			return 1;
	}
	return 0;
}

int main()
{
	
	int left_step  = 1;//初始每段化长度
	int up_step    = 2;
	int right_step = 2;
	int down_step  = 1;
	scanf("%d%d", &x, &y);
	while(now.x != x || now.y != y)
	{
		if(turn_down_line(down_step))
			break;
		if(turn_left_line(left_step))
			break;
		if(turn_up_line(up_step))
			break;
		if(turn_right_line(right_step))
			break;
		down_step += 2;
		left_step += 2;
		up_step += 2;
		right_step += 2;
	}
	printf("%d", len);
	return 0;
}