Cyclic Redundancy Check, CRC

一.写在前面

循环冗余校验(Cyclic Redundancy Check, CRC)是一种根据网络数据包或电脑文件等数据产生简短固定位数校验码的一种散列函数，主要用来检测或校验数据传输或者保存后可能出现的错误。它是利用除法及余数的原理来作错误侦测的。

二.简单原理

CRC码是基于模2运算而建立编码规律的校验码。模2运算的特点是不考虑敬畏和借位的运算，其规律如下：

1. 模2加和模2减法结果相等的，即0+1=0，0-1=0；0+0=0，0-0=0；1+0=0，1-0=0；1+1=0，1-1=0；可见啷个数的模2和恒为0.
2. 模2乘是按模2和求部分积之和。
3. 模2除是按模2减求部分余数。每求一位商应使部分余数减少一位。上商的原则是：当部分余数的首位为1时，上商1；当部分余数的首部为0时，上商0。当部分余数的位数小于被除数的位数时，该余数即为最后的余数。

基本思想为：原始信息mx 和生成多项式gx，先求出余数的位数即gx的位数-1。然后再mx后面拼接和余数位数相等的0.之后就使用mx/gx（注意这里是模2运算），当部分余数的位数小于被除数的位数时，该余数即为最后的余数。

三.编码实现(C++)

// CRC.cpp 

#include <iostream>
using namespace std;

//CRC编码
string crc_encode(string raw_data, string gx)
{
	string crc_data = raw_data;
	//在原生数据的后面追加gx长度-1个0
	for (uint8_t i = 0; i < gx.length() - 1; i++)
	{
		raw_data += "0";
	}

	string quo = "";//存放商

	//按位异或
	for (uint8_t i = 0; i < raw_data.length(); i++)
	{
		//如果最高位为1则上1
		if (raw_data[i] == '1')
		{
			quo += '1';
			for (uint8_t j = 0; j < gx.length(); j++)
			{
				if ((raw_data[i + j] - 48) ^ (gx[j] - 48))
				{
					raw_data[i + j] = '1';
				}
				else
				{
					raw_data[i + j] = '0';
				}
			}
		}
		//如果最高位为0则上0
		else
		{
			quo += '0';
			for (uint8_t j = 0; j < gx.length(); j++)
			{
				if ((raw_data[i + j] - 48) ^ 0)
				{
					raw_data[i + j] = '1';
				}
				else
				{
					raw_data[i + j] = '0';
				}
			}
		}
		//结束出操作标志
		if (quo.length() == raw_data.length() - gx.length() + 1)
		{
			break;
		}
	}
	//此时CRC校验码已经在raw_data的末尾，只要拼接到crc_data后即可
	crc_data += raw_data.substr(crc_data.length(), gx.length() - 1);
	return crc_data;
}

//CRC解码
//rem为余数 引用传递，当检查有错时函数返回false且rem值为含有1的余数字符串
//可以根据余数rem的值纠错，但这取决于gx所以无法在此函数中直接纠正
bool crc_check(string crc_data, string gx, string &rem)
{

	string quo = "";//存放商
	//按位异或
	for (uint8_t i = 0; i < crc_data.length(); i++)
	{
		//如果最高位为1则上1
		if (crc_data[i] == '1')
		{
			quo += '1';
			for (uint8_t j = 0; j < gx.length(); j++)
			{
				if ((crc_data[i + j] - 48) ^ (gx[j] - 48))
				{
					crc_data[i + j] = '1';
				}
				else
				{
					crc_data[i + j] = '0';
				}
			}
		}
		//如果最高位为0则上0
		else
		{
			quo += '0';
			for (uint8_t j = 0; j < gx.length(); j++)
			{
				if ((crc_data[i + j] - 48) ^ 0)
				{
					crc_data[i + j] = '1';
				}
				else
				{
					crc_data[i + j] = '0';
				}
			}
		}
		//结束出操作标志
		if (quo.length() == crc_data.length() - gx.length() + 1)
		{
			break;
		}
	}
	rem = crc_data.substr(crc_data.length() - gx.length()+1, gx.length()-1);

	//此时检查rem的值是否全为0;如果全为0则校验通过否则出错
	bool error = false;
	for (uint8_t i = 0; i < rem.length(); i++)
	{
		if (rem[i] != '0')
		{
			error = true;
			break;
		}
	}
	if (error)
		return false;
	else
		return true;
}

int main()
{
	string raw_data = "110";
	string gx = "11011";
	string rem = "";
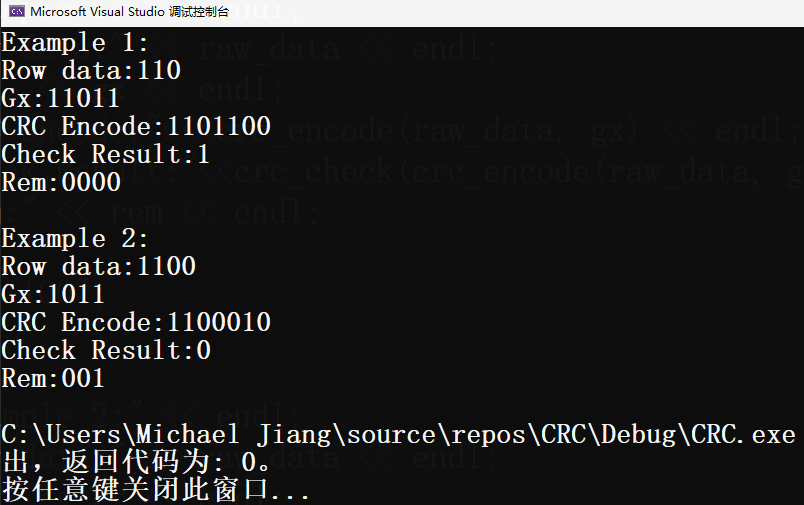
	cout << "Example 1:" << endl;
	cout << "Row data:" << raw_data << endl;
	cout << "Gx:" << gx << endl;
	cout << "CRC Encode:" <<crc_encode(raw_data, gx) << endl;
	cout << "Check Result:"<<crc_check(crc_encode(raw_data, gx), gx, rem) << endl;
	cout << "Rem:" << rem << endl;

	raw_data = "1100";
	gx = "1011";
	cout << "\n";
	cout << "Example 2:" << endl;
	cout << "Row data:" << raw_data << endl;
	cout << "Gx:" << gx << endl;
	cout << "CRC Encode:" << crc_encode(raw_data, gx) << endl;
	cout << "Check Result:" << crc_check("1100011", gx, rem) << endl;
	cout << "Rem:" << rem << endl;
}

结果：

Github->https://github.com/MichaelJiang1997/CRC