众所周知 algorithm 头文件 里有两个函数
next_permutation()
prev_permutation()使用它们可以很方便的生成给定范围内的组合数。
首先尝试使用递归实现这个next_permutation()函数:
#include "cstdio"
int cnt = 0;
void per(int data[], int k)
{
if(k >= 4)
{
printf("%d%d%d%d\n", data[0], data[1], data[2], data[3]);
cnt++;
return;
}
for(int i = k; i < 4; i++)
{
std::swap(data[i], data[k]);
per(data, k + 1);
std::swap(data[i], data[k]);
}
}
int main()
{
int data[] = {1, 2, 3, 4};
per(data, 0);
printf("Total:%d", cnt);
return 0;
}结果如下:
1234
1243
1324
1342
1432
1423
2134
2143
2314
2341
2431
2413
3214
3241
3124
3142
3412
3421
4231
4213
4321
4312
4132
4123
Total:24
实战一下:
// 问题描述
// 100 可以表示为带分数的形式:100 = 3 + 69258 / 714。
// 还可以表示为:100 = 82 + 3546 / 197。
// 注意特征:带分数中,数字1~9分别出现且只出现一次(不包含0)。
// 类似这样的带分数,100 有 11 种表示法。
// 输入格式
// 从标准输入读入一个正整数N (N<1000*1000)
// 输出格式
// 程序输出该数字用数码1~9不重复不遗漏地组成带分数表示的全部种数。
// 注意:不要求输出每个表示,只统计有多少表示法!
// 样例输入1
// 100
// 样例输出1
// 11
// 样例输入2
// 105
// 样例输出2
// 6
思路:
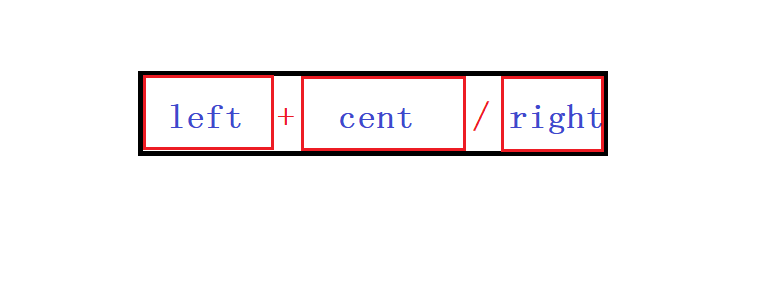
题目要求 1 ~ 9 数字全部出现;这时我们可以使用组合数来产生所有可能的组合
用加号和除号将组合数分成三个部分(如图所示)
对于某一个具体的组合数只要使用两个for循环来遍历这个组合数就可以得到这个组合数所有的可能
并和输入值res比较即可得出答案
#include "cstdio"
#include "algorithm"
using namespace std;
int num[] = {1, 2, 3, 4, 5, 6, 7, 8, 9};
int cnt = 0;
int res = 0, left = 0, cent = 0, right = 0;
int to_int(int i, int j)//将组合数某个范围内的数字转INT
{
int r = 0;
int k = 1;
for(; j >=i; j--)
{
r += num[j] * k;
k *= 10;
}
return r;
}
void div()//分割函数
{
for(int i = 0; i <= 6; i++)// 分割+
{
for(int j = i+1; j <= 7; j++)// 分割/
{
left = to_int(0, i);
cent = to_int(i+1, j);
right = to_int(j+1, 8);
if(res * right == left * right + cent )//这里转化了一下表达式避免使用 / 所带来的精度问题
{
printf("%d = %d + %d / %d\n", res, left, cent, right);
cnt++;
}
}
}
}
int main()
{
scanf("%d", &res);
do{
div();
}while(next_permutation(num, num + 9));
printf("Total:%d", cnt);
return 0;
}输入:100
输出如下:
100 = 3 + 69258 / 714
100 = 81 + 5643 / 297
100 = 81 + 7524 / 396
100 = 82 + 3546 / 197
100 = 91 + 5742 / 638
100 = 91 + 5823 / 647
100 = 91 + 7524 / 836
100 = 94 + 1578 / 263
100 = 96 + 1428 / 357
100 = 96 + 1752 / 438
100 = 96 + 2148 / 537
Total:11